Matematika A razina
-
O ispitu matematike više razine na maturi
Lekcija 1: O državnoj maturi3 teme -
Lekcija 2: Priprema za ispit matematike više razine5 teme
-
Osnove aritmetikeLekcija 3: Terminologija
-
Lekcija 4: Skupovi brojeva4 teme|5 Kvizovi
-
Skupovi brojeva
-
Računske operacije među skupovima
-
Prosti i složeni brojevi, najveći zajednički djelitelj (NZD) i najmanji zajednički višekratnik (NZV)
-
Dijeljenje s ostatkom
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 1
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 2
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 3
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 4
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 5
-
Skupovi brojeva
-
Lekcija 5: Racionalni brojevi i brojevni pravac2 teme|5 Kvizovi
-
Oblici zapisa racionalnih brojeva
-
Uspoređivanje brojeva na brojevnom pravcu, uspoređivanje decimalnih brojeva i zaokruživanje
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 1
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 2
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 3
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 4
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 5
-
Oblici zapisa racionalnih brojeva
-
Lekcija 6: Omjeri, postotci, apsolutna vrijednost i aritmetička sredina3 teme|5 Kvizovi
-
Omjeri, produljeni omjeri, postotci i promili
-
Apsolutna vrijednost, aritmetička sredina i primjena u jednostavnim zadacima
-
Proporcionalnost
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 1
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 2
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 3
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 4
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 5
-
Omjeri, produljeni omjeri, postotci i promili
-
Lekcija 7: Potencije i znanstveni zapis broja3 teme|5 Kvizovi
-
Definicija potencije, osnovna pravila računanja s potencijama
-
Primjena potencija u znanstvenom zapisu broja (veliki i mali brojevi)
-
Vježbe s primjenom u svakodnevnim situacijama
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 1
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 2
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 3
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 4
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 5
-
Definicija potencije, osnovna pravila računanja s potencijama
-
Lekcija 8: Kompleksni brojevi i Gaussova ravnina
-
Lekcija 9: Osnove statistike
-
Osnove algebreLekcija 10: Algebarski izrazi3 teme|5 Kvizovi
-
Lekcija 11: Algebarski razlomci i intervali3 teme|5 Kvizovi
-
Skraćivanje algebarskih razlomaka
-
Množenje, dijeljenje, zbrajanje i oduzimanje algebarskih razlomaka
-
Uspoređivanje brojeva na brojevnom pravcu, intervali, unija i presjek intervala
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 1
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 2
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 3
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 4
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 5
-
Skraćivanje algebarskih razlomaka
-
Lekcija 12: Linearne jednadžbe3 teme|5 Kvizovi
-
Lekcija 13: Sustavi linearnih jednadžbi2 teme|5 Kvizovi
-
Lekcija 14: Linearne nejednadžbe2 teme|5 Kvizovi
-
Rješavanje linearnih nejednadžbi i prikaz rješenja na pravcu
-
Sustavi linearnih nejednadžbi i nejednadžbe s apsolutnom vrijednošću
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 1
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 2
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 3
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 4
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 5
-
Rješavanje linearnih nejednadžbi i prikaz rješenja na pravcu
-
Lekcija 15: Nizovi5 teme
-
FunkcijeLekcija 16: Osnove funkcija3 teme
-
Lekcija 17: Kvadratna funkcija4 teme|5 Kvizovi
-
Lekcija 18: Eksponencijalne i logaritamske funkcije2 teme
-
Lekcija 19: Trigonometrijske funkcije5 teme
-
Lekcija 20: Svojstva funkcija3 teme
-
Lekcija 21: Derivacije
-
Analitička geometrijaLekcija 22: Koordinatna ravnina i udaljenost točaka
-
Lekcija 23: Kružnice u koordinatnom sustavu
-
Lekcija 24: Vektori i skalari
-
Geometrija ravnine - PlanimetrijaLekcija 25: Kut
-
Lekcija 26: Trokuti
-
Lekcija 27: Pravokutni trokut
-
Lekcija 28: Trigonometrija u pravokutnom trokutu
-
Lekcija 29: Kvadrat i pravokutnik
-
Lekcija 30: Romb, paralelogram i trapez
-
Lekcija 31: Mnogokuti
-
Lekcija 32: Trigonometrija trokuta
-
Lekcija 33: Kružnica
-
Geometrija prostoraLekcija 34: Prizme
-
Lekcija 35: Kocka i kvadar
-
Lekcija 36: Piramide
-
Lekcija 37: Valjak
-
Lekcija 38: Stožac
-
Lekcija 39: Kugla
Lekcija 3: Terminologija
Lekcija 3: Terminologija
Pojmovi i činjenice koje trebate znati za nastavak tečaja
U ovoj lekciji donosimo pregled najvažnijih matematičkih pojmova i činjenica koji se često koriste u daljnjem gradivu. Razumijevanje ovih termina olakšat će rješavanje zadataka i praćenje naprednijih tema. Iako se neke definicije čine osnovnima, važno je imati čvrste temelje kako biste bez poteškoća savladali zahtjevnije dijelove gradiva.
1. Osnovne operacije i svojstva
Adicija (zbrajanje)
- Definicija: Operacija kojom se dvije ili više vrijednosti (brojevi, polinomi itd.) zbrajaju u jednu rezultantnu vrijednost (zbroj).
- Svojstva:
- Komutativnost:
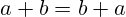
- Asocijativnost:
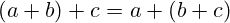
- Komutativnost:
Aritmetika
- Što obuhvaća: Bavi se brojevima (najčešće prirodnim, cijelim, racionalnim) i osnovnim računskim operacijama: zbrajanje, oduzimanje, množenje, dijeljenje.
- Zašto je važna: Smatra se “kraljicom matematike” jer čini osnovu za daljnje računske i algebraičke koncepte.
Komutativnost
- Definicija: Svojstvo kod kojeg se redoslijed operanada može zamijeniti, a rezultat ostaje isti (npr.
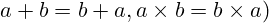 .
. - Primjena: Vrijedi za zbrajanje i množenje realnih brojeva, no ne vrijedi za oduzimanje ili dijeljenje.
Asocijativnost (udruživanje)
- Definicija: Svojstvo računske operacije kod koje način grupiranja operanada ne mijenja krajnji rezultat (npr.
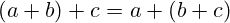 ).
). - Primjeri: Zbrajanje, množenje realnih brojeva.
Distributivnost
- Definicija: Svojstvo po kojem množenje “distribuira” zbrajanje:
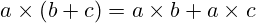 .
. - Važnost: Omogućuje razvijanje algebarskih izraza (npr. proširivanje zagrada).
2. Temeljni pojmovi iz algebre
Algebra
- Što proučava: Granа matematike koja se, uz brojeve, bavi i općim oznakama (simbolima, nepoznanicama, varijablama).
- Važnost: Osim rješavanja jednadžbi i nejednadžbi, algebra uključuje i koncept funkcija, polinoma, sustava jednadžbi, matrica, vektorskih prostora i sl.
Binom
- Definicija: Algebarski izraz sastavljen od dvaju članova povezanih zbrajanjem ili oduzimanjem (npr.
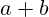 ,
, 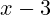 ).
). - Kvadrat binoma:
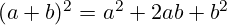 .
.
Trinom
- Definicija: Algebarski izraz s tri člana (npr.
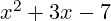 ).
). - Važnost: Čest je u kvadratnim jednadžbama i funkcijama.
Monom
- Definicija: Algebarski izraz koji se sastoji od jednog jedinog člana, obično oblika
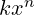 (npr.
(npr. 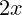 ,
, 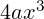 ,
, 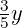 ).
). - Primjena: Osnova pri definiranju polinoma i pojednostavljivanju algebarskih izraza.
Binomni koeficijenti
- Definicija: Koeficijenti koji se javljaju u ekspanziji
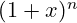 , često označeni kao
, često označeni kao 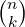 .
. - Mjesto pojavljivanja: Važni su u Pascalovu trokutu, kombinatorici i statistici (npr. binomna raspodjela).
Polinom
- U užem smislu: Algebarski izraz oblika
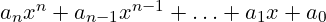 , gdje su
, gdje su 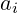 koeficijenti, a
koeficijenti, a 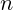 je konačan.
je konačan. - Primjena: U rješavanju jednadžbi višeg stupnja, analizi funkcija, modeliranju u prirodnim i tehničkim znanostima.
3. Brojevi i njihova svojstva
Brojevni sustavi
- Poziocijski i nepoziocijski:
- Poziocijski (dekadski, binarni) – vrijednost znamenke ovisi o njezinu mjestu (poziciji).
- Nepoziocijski (rimski brojevi) – svakom simbolu dodijeljena je unaprijed zadana vrijednost, neovisno o položaju.
- Najčešći u praksi: Dekadski sustav (baziran na broju 10).
Racionalni i iracionalni brojevi
- Racionalni: Mogu se izraziti u obliku
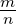 (gdje je
(gdje je 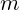 i
i 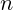 cijeli broj,
cijeli broj, 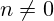 ).
). - Iracionalni: Nije ih moguće izraziti omjerom dvaju cijelih brojeva (npr.
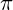 ,
, 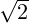 ). Njihov decimalni zapis je beskonačan i neperiodičan.
). Njihov decimalni zapis je beskonačan i neperiodičan.
Aproksimacija
- Definicija: Približno izračunavanje ili zapisivanje neke vrijednosti kada je točno rješenje nezgodno ili prekomplicirano (npr.
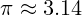 ).
). - Primjena: Svakodnevni izračuni (npr. zaokruživanje) ili numeričke metode u naprednijim temama.
Najveći zajednički djelitelj (NZD) i najmanji zajednički višekratnik (NZV)
- NZD (npr.
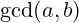 ): Najveći prirodni broj koji istovremeno dijeli i
): Najveći prirodni broj koji istovremeno dijeli i 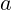 i
i 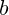 .
. - NZV (npr.
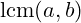 ): Najmanji prirodni broj koji je višekratnik i
): Najmanji prirodni broj koji je višekratnik i 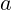 i
i 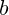 .
.
Postotak i promil
- Postotak: Stoti dio neke vrijednosti (
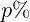 ). Na primjer, 5% od 300 je
). Na primjer, 5% od 300 je 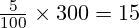 .
. - Promil: Tisućiti dio (‰). Npr. 7‰ od 1000 iznosi 7.
4. Relacije, skupovi i elementi
Skup
- Definicija: Temeljni pojam matematičke teorije skupova; predstavlja kolekciju različitih objekata nazvanih elementima skupa.
- Primjeri:
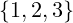 , skup realnih brojeva
, skup realnih brojeva 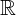 , skup svih učenika nekog razreda.
, skup svih učenika nekog razreda.
Element
- Označavanje: Kažemo “
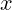 je element skupa
je element skupa 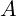 ” i pišemo
” i pišemo 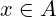 .
. - Intuitivno značenje: Svaki objekt koji pripada skupu.
Disjunktni skupovi
- Definicija: Skupovi koji nemaju zajedničkih elemenata; tj.
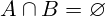 .
. - Primjer: Skup svih parnih i skup svih neparnih cijelih brojeva.
Razmjer (proporcija)
- Definicija: Jedna jednakost dvaju ili više omjera (
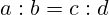 ).
). - Važnost: Koristi se pri usporedbi veličina, sličnosti trokuta, rješavanju praktičnih problema (postotci, mjerenje itd.).
5. Dodatni ključni pojmovi
Dijeljenje
- Definicija: Operacija suprotna množenju, traži koliko je puta jedan broj (dijeljenik) sadržan u drugome (dijelitelj).
- Rezultat: Kvocijent, ponekad i s ostatkom.
Periodični decimalni brojevi
- Definicija: Decimalni brojevi koji nakon nekog mjesta imaju ponavljajući niz znamenaka (npr. 0.333…, 1.272727…).
- Primjer:
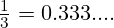
Pravila djeljivosti
- Primjer: Broj je djeljiv s 2 ako je zadnja znamenka paran broj. Broj je djeljiv s 3 ako je zbroj znamenaka djeljiv s 3, itd.
- Upotreba: Olakšava provjeru dijeli li neki broj drugi broj bez potrebe za “dugim dijeljenjem”.
Konstanta i varijabla
- Konstanta: Vrijednost koja se ne mijenja tijekom problema ili funkcije (npr.
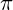 , neke zadane numeričke veličine).
, neke zadane numeričke veličine). - Varijabla: Veličina koja se može mijenjati (npr.
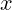 u funkciji
u funkciji 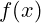 ).
).
Razlomak
- Definicija: Omjer dvaju brojeva
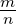 . Pri čemu je m (brojnik) podijeljen s n (nazivnik), uz uvjet
. Pri čemu je m (brojnik) podijeljen s n (nazivnik), uz uvjet 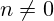 .
. - Svojstva: Može se proširivati (umnožiti brojnik i nazivnik istim brojem) ili skraćivati (podijeliti brojnik i nazivnik zajedničkim djeliteljem).
Zaključak
Ova terminologija obuhvaća pojmove iz aritmetike, algebre i teorije brojeva koje ćete često susretati u sljedećim lekcijama i zadacima. Preporučujemo da povremeno pregledate ove definicije kako biste imali čvrst temelj za razumijevanje naprednijih tema, poput funkcija, derivacija, trigonometrijskih jednadžbi ili analitičke geometrije.
Ako vam je neki pojam nejasan, vratite se na ovu listu ili ga potražite u dodatnim izvorima. Temeljito poznavanje osnovne matematičke terminologije olakšat će vam napredovanje kroz cjelokupni program pripreme!
