Matematika A razina
-
O ispitu matematike više razine na maturi
Lekcija 1: O državnoj maturi3 teme -
Lekcija 2: Priprema za ispit matematike više razine5 teme
-
Osnove aritmetikeLekcija 3: Terminologija
-
Lekcija 4: Skupovi brojeva4 teme|5 Kvizovi
-
Skupovi brojeva
-
Računske operacije među skupovima
-
Prosti i složeni brojevi, najveći zajednički djelitelj (NZD) i najmanji zajednički višekratnik (NZV)
-
Dijeljenje s ostatkom
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 1
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 2
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 3
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 4
-
Matematika - Skupovi brojeva i osnovne računske operacije - Domaća zadaća 5
-
Skupovi brojeva
-
Lekcija 5: Racionalni brojevi i brojevni pravac2 teme|5 Kvizovi
-
Oblici zapisa racionalnih brojeva
-
Uspoređivanje brojeva na brojevnom pravcu, uspoređivanje decimalnih brojeva i zaokruživanje
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 1
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 2
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 3
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 4
-
Matematika - Racionalni brojevi i njihov prikaz - Domaća zadaća 5
-
Oblici zapisa racionalnih brojeva
-
Lekcija 6: Omjeri, postotci, apsolutna vrijednost i aritmetička sredina3 teme|5 Kvizovi
-
Omjeri, produljeni omjeri, postotci i promili
-
Apsolutna vrijednost, aritmetička sredina i primjena u jednostavnim zadacima
-
Proporcionalnost
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 1
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 2
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 3
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 4
-
Matematika - Omjeri, postoci i proporcionalnost - Domaća zadaća 5
-
Omjeri, produljeni omjeri, postotci i promili
-
Lekcija 7: Potencije i znanstveni zapis broja3 teme|5 Kvizovi
-
Definicija potencije, osnovna pravila računanja s potencijama
-
Primjena potencija u znanstvenom zapisu broja (veliki i mali brojevi)
-
Vježbe s primjenom u svakodnevnim situacijama
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 1
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 2
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 3
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 4
-
Matematika - Potencije i znanstveni zapis broja - Domaća zadaća 5
-
Definicija potencije, osnovna pravila računanja s potencijama
-
Lekcija 8: Kompleksni brojevi i Gaussova ravnina
-
Lekcija 9: Osnove statistike
-
Osnove algebreLekcija 10: Algebarski izrazi3 teme|5 Kvizovi
-
Lekcija 11: Algebarski razlomci i intervali3 teme|5 Kvizovi
-
Skraćivanje algebarskih razlomaka
-
Množenje, dijeljenje, zbrajanje i oduzimanje algebarskih razlomaka
-
Uspoređivanje brojeva na brojevnom pravcu, intervali, unija i presjek intervala
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 1
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 2
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 3
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 4
-
Matematika - Algebarski razlomci i intervali - Domaća zadaća 5
-
Skraćivanje algebarskih razlomaka
-
Lekcija 12: Linearne jednadžbe3 teme|5 Kvizovi
-
Lekcija 13: Sustavi linearnih jednadžbi2 teme|5 Kvizovi
-
Lekcija 14: Linearne nejednadžbe2 teme|5 Kvizovi
-
Rješavanje linearnih nejednadžbi i prikaz rješenja na pravcu
-
Sustavi linearnih nejednadžbi i nejednadžbe s apsolutnom vrijednošću
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 1
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 2
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 3
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 4
-
Matematika - Linearne nejednadžbe i sustavi nejednadžbi - Domaća zadaća 5
-
Rješavanje linearnih nejednadžbi i prikaz rješenja na pravcu
-
Lekcija 15: Nizovi5 teme
-
FunkcijeLekcija 16: Osnove funkcija3 teme
-
Lekcija 17: Kvadratna funkcija4 teme|5 Kvizovi
-
Lekcija 18: Eksponencijalne i logaritamske funkcije2 teme
-
Lekcija 19: Trigonometrijske funkcije5 teme
-
Lekcija 20: Svojstva funkcija3 teme
-
Lekcija 21: Derivacije
-
Analitička geometrijaLekcija 22: Koordinatna ravnina i udaljenost točaka
-
Lekcija 23: Kružnice u koordinatnom sustavu
-
Lekcija 24: Vektori i skalari
-
Geometrija ravnine - PlanimetrijaLekcija 25: Kut
-
Lekcija 26: Trokuti
-
Lekcija 27: Pravokutni trokut
-
Lekcija 28: Trigonometrija u pravokutnom trokutu
-
Lekcija 29: Kvadrat i pravokutnik
-
Lekcija 30: Romb, paralelogram i trapez
-
Lekcija 31: Mnogokuti
-
Lekcija 32: Trigonometrija trokuta
-
Lekcija 33: Kružnica
-
Geometrija prostoraLekcija 34: Prizme
-
Lekcija 35: Kocka i kvadar
-
Lekcija 36: Piramide
-
Lekcija 37: Valjak
-
Lekcija 38: Stožac
-
Lekcija 39: Kugla
Računske operacije među skupovima
U ovoj lekciji istražit ćemo osnovne odnose i računske operacije koje se mogu provoditi nad skupovima: uniju, presjek, razliku, komplement, te pojmove podskupa i kardinalnog broja. Razumijevanje ovih operacija i pojmova ključno je za daljnji rad u matematici, posebno kada se bavimo logičkim i skupovnim zadacima ili složenijim strukturama.
1. Podskup i univerzalni skup
1.1 Podskup
Kažemo da je skup A podskup skupa B ako svaki element skupa A ujedno pripada skupu B. Drugim riječima, nema elementa u A koji se ne nalazi u B.
Oznaka:
![]()
Primjer: Ako je A = {1, 2} i B = {1,2,3}, tada vrijedi
![]()
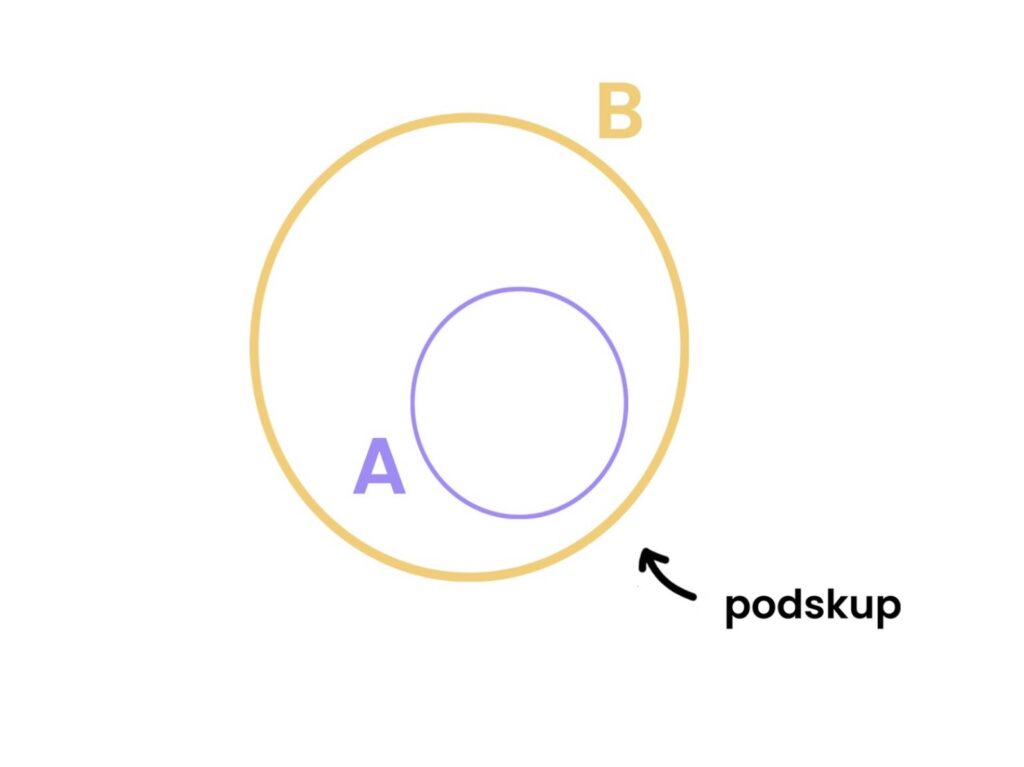
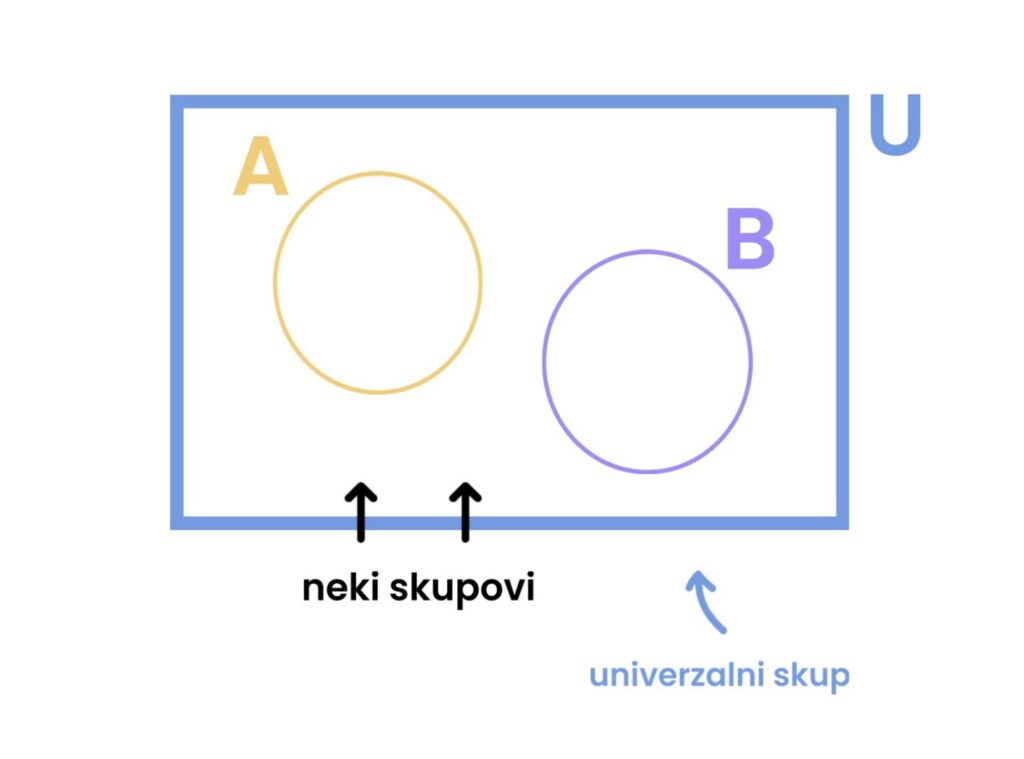
1.2 Univerzalni skup
Ako unutar nekog “okvira” ili konteksta (npr. ako govorimo samo o prirodnim brojevima) promatramo odnose među njegovim podskupovima, onda taj “okvir” nazivamo univerzalni skup. Označavamo ga s U.
Primjer: Ako je zadani univerzum ili “okvir” U = {1,2,3,4,5}, svaki drugi skup koji uzmemo za promatranje (npr. {1,4}) možemo smatrati podskupom unutar tog univerzuma.
2. Unija, presjek i disjunktni skupovi
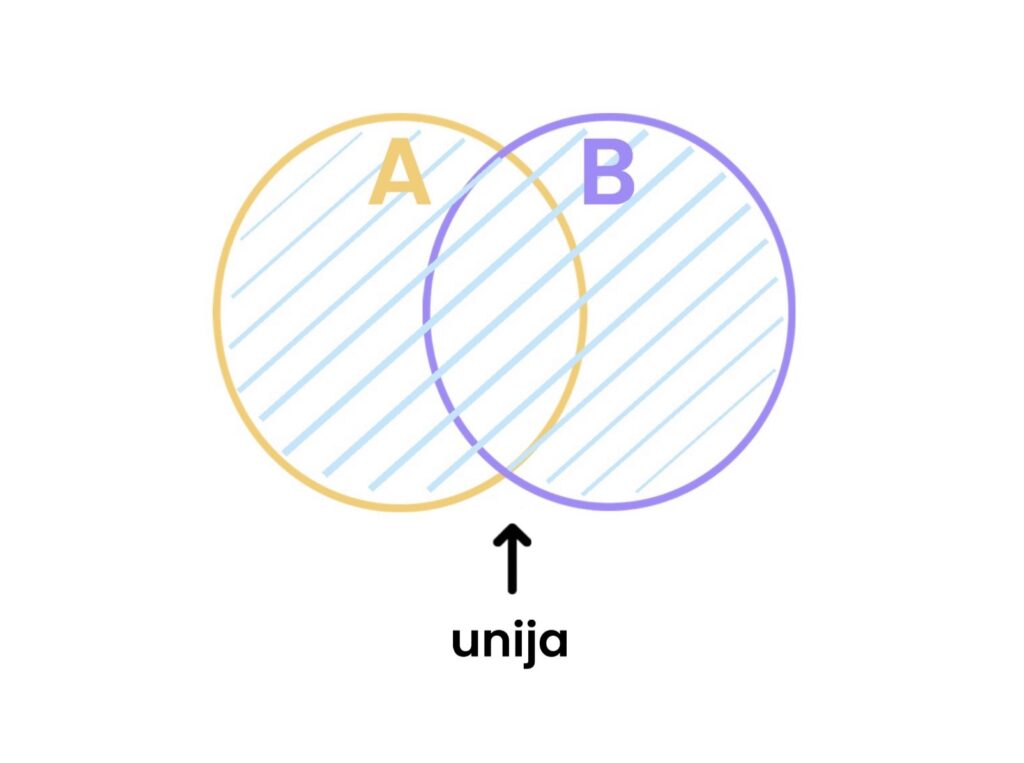
2.1 Unija skupova
Unija dvaju skupova A i B definira se kao skup svih elemenata koji pripadaju barem jednom od tih skupova.
Oznaka:
![]()
Primjer: Ako je A = {1,2}, a B = {2,3}, tada
![]()
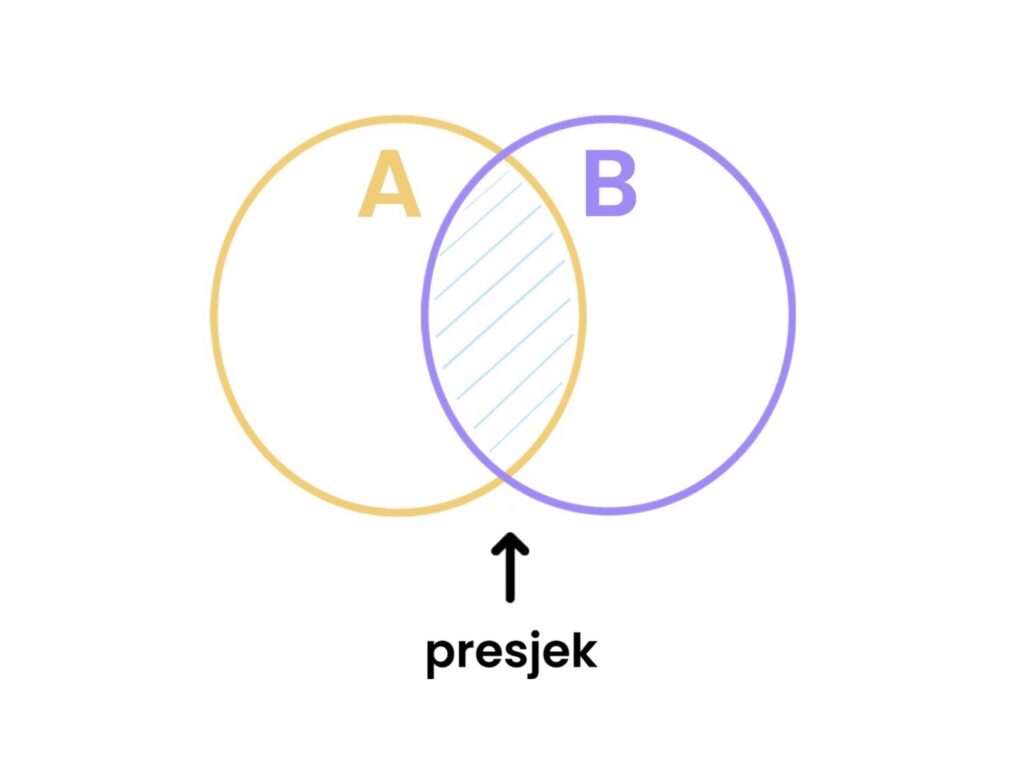
2.2 Presjek skupova
Presjek dvaju skupova A i B definira se kao skup svih elemenata koji pripadaju istovremeno i skupu A i skupu B.
Oznaka:
![]()
Primjer: Ako je A = {1,2}, a B = {2,3}, tada
![]()
2.3 Disjunktni skupovi
Skupovi A i B su disjunktni ako nemaju zajedničkih elemenata u presjeku. Drugim riječima,
![]()

Primjer: Ako je A = {1,2}, a B = {3,4}, tada je
![]()
pa su A i B disjunktni skupovi.
3. Razlika i komplement
3.1 Razlika skupova
Razlika skupova A i B definira se kao skup svih elemenata koji se nalaze u skupu A, ali ne u skupu B.
Oznaka:
![]()
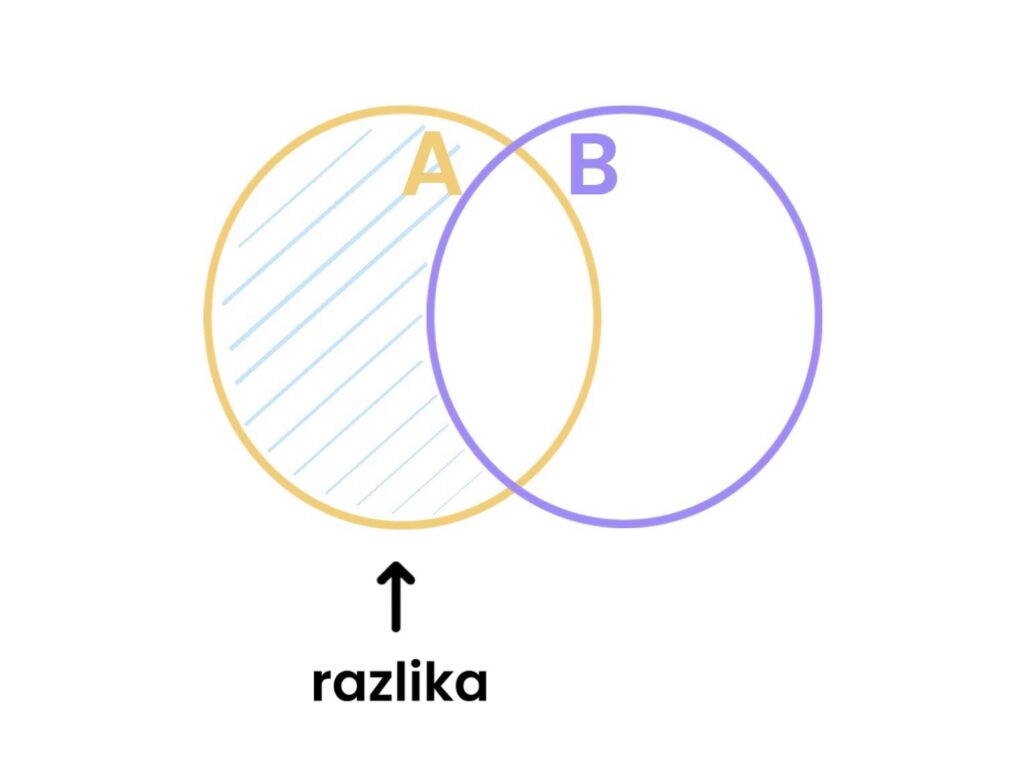
Primjer: Ako je A = {1,2,3}, a B = {2,4}, tada
![]()
3.2 Komplement skupa
Ako je A podskup od U, komplement skupa A je skup svih elemenata univerzalnog skupa koji se ne nalaze u A.
Oznaka:
![]()
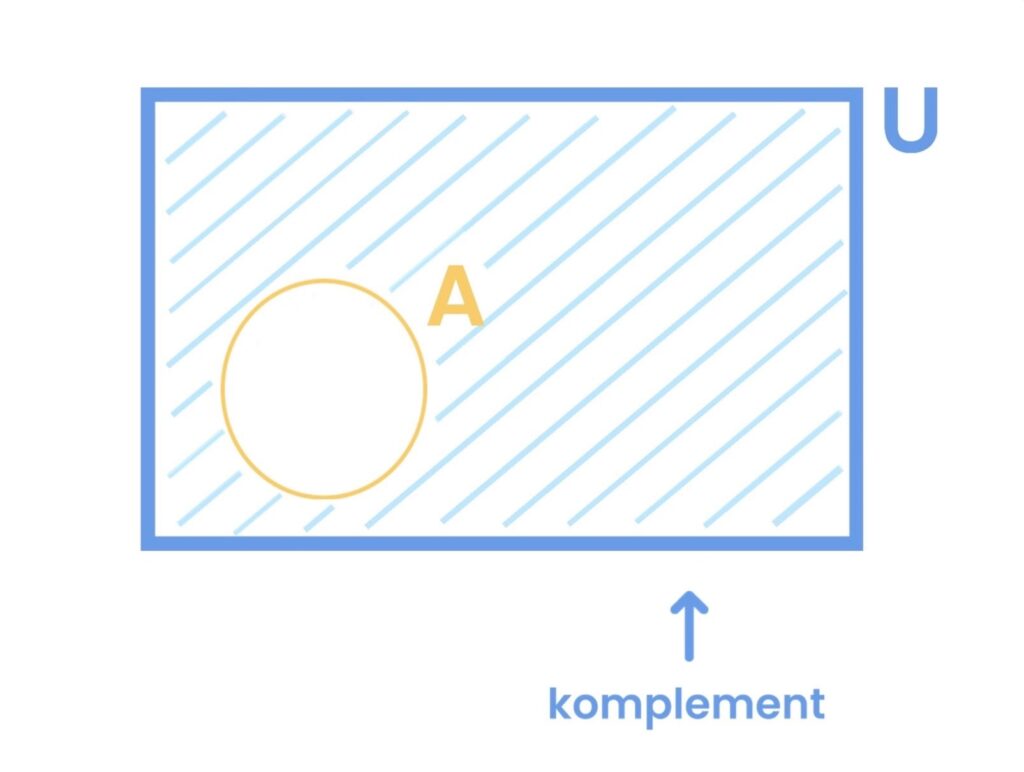
Primjer: Ako je U = {1,2,3,4} i A = {2,3}, tada
![]()
4. Kardinalni broj skupa i prazan skup
4.1 Kardinalni broj skupa
Kardinalni broj (ili veličina) skupa S označavamo s card(S) i on predstavlja broj elemenata tog skupa.
Primjer: Ako je S = {2,4,6}, tada je card(S) = 3.
4.2 Prazan skup
Prazan skup je skup bez ijednog elementa. Za njega uvijek vrijedi card(S) = 0.
Oznaka:
![]()
Primjer:
![]()
može biti prazan skup ako A i B nemaju zajedničkih elemenata.
5. Zašto su ove operacije važne?
- Računske operacije među skupovima daju temelj za logičko zaključivanje, rješavanje problema u kombinatorici i razumijevanje složenih matematičkih struktura.
- Pojmovi unije, presjeka i razlike često se primjenjuju u množinama, funkcijama, vjerojatnosti (gdje koristimo događaje umjesto skupova) i drugim granama matematike.
- Kardinalni broj presudno je važan u kombinatorici, statistikama i pri analiziranju konačnih skupova.
Ovim smo obuhvatili ključne pojmove računa sa skupovima: od podskupa i univerzalnog skupa, preko unije, presjeka i razlike, do komplementa i kardinalnog broja. U sljedećim ćemo lekcijama vidjeti kako se ovi koncepti koriste u složenijim matematičkim zadacima i situacijama.

Responses