Matematika A razina Lekcija 4: Skupovi brojeva Skupovi brojeva

Lekcija 4, Tema 1

U tijeku

← Previous Next→

Skupovi brojeva

Lekcija Progress

0% Complete

Lekcija 1, Dio 1: Skupovi brojeva (prirodni, cijeli, racionalni, iracionalni, realni)

U matematici se brojni sustavi postupno proširuju kako bismo mogli opisati i rješavati sve složenije zadatke. Različite vrste brojeva grupiramo u skupove brojeva, pri čemu svaki prošireni skup sadrži prethodne. Na taj način imamo hijerarhiju od najužeg do najšireg skupa brojeva.

Što je skup?
Skup možemo shvatiti kao kolekciju međusobno različitih objekata. Svaki se pojedini objekt u skupu naziva element toga skupa. Primjerice, skup {1,3,5} sadrži tri elementa: 1, 3 i 5.

U kontekstu brojeva, skupovi brojeva su klasifikacije koje nam omogućuju da razumijemo koje brojeve koristimo i kako se oni međusobno odnose.

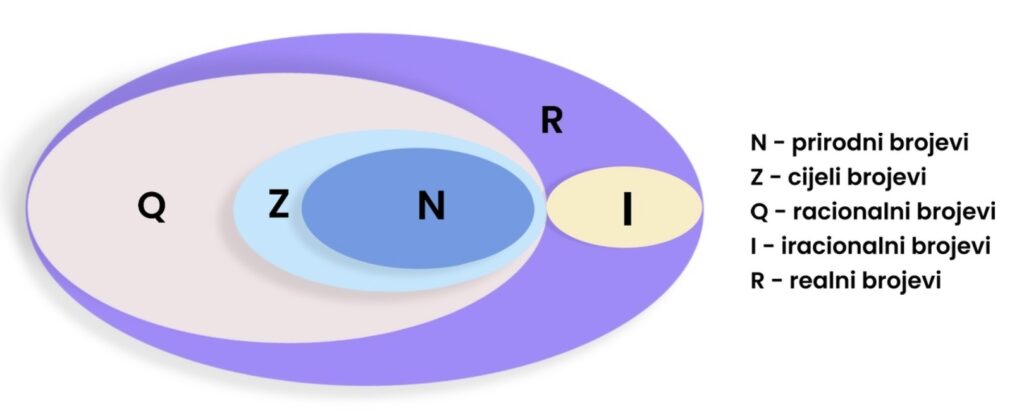
Prirodni brojevi (N)

Definicija: Prirodni brojevi su brojevi koje dobivamo brojanjem “od jedan naviše”.
Primjeri: 1, 2, 3, 4, 5,
Ovaj skup označavamo s N i može se zapisati kao:

$N={1,2,3,4,\ldots\thinsp}$

Prirodni brojevi koriste se za brojanje predmeta i izvođenje osnovnih računski operacija. Najčešće su nam prva i najintuitivnija vrsta brojeva s kojom se susrećemo.

Cijeli brojevi (Z)

Definicija: Cijeli brojevi obuhvaćaju sve prirodne brojeve, nulu i sve njihove negativne pandane.
Primjeri: , -3, -2, -1, 0, 1, 2, 3,
Ovaj skup označavamo s Z:

$Z={\ldots,-3,-2,-1,0,1,2,3,\ldots\thinsp}$

Uvođenjem negativnih brojeva proširujemo mogućnosti računanja. Sada ne samo da možemo brojati i zbrajati, već i izražavati dugove, manjkove ili promjene vrijednosti prema dolje.

Racionalni brojevi (Q)

Definicija: Racionalni brojevi su svi brojevi koji se mogu zapisati u obliku razlomka,

$\frac{m}{n}$

gdje je M cijeli broj, a N prirodni broj različit od nule. Primjeri:

$-\frac{1}{2},\frac{3}{4},\frac{7}{1}=7,0.25=\frac{1}{4}$

Skup racionalnih brojeva označavamo s Q:

$Q=\left\{\frac{m}{n}\mid m\in Z,n\in N\setminus{0}\right\}$

Racionalni brojevi uključuju sve poznate razlomke, ali i sve cijele brojeve, budući da je svaki cijeli broj moguće zapisati kao razlomak. Oni nam omogućuju precizno iskazivanje dijelova cjeline, postotaka i udjela.

Iracionalni brojevi (I)

Definicija: Iracionalni brojevi su oni brojevi koje ne možemo prikazati kao razlomak dvaju cijelih brojeva. Imaju beskonačan, neperiodičan decimalni zapis.

Primjeri:

$\sqrt2,\pi,e$

Skup iracionalnih brojeva označavamo s I (veliko i).

Iracionalni brojevi omogućuju nam opisivanje dužina, površina i omjera koji se ne mogu točno izraziti razlomcima, čime se širi opseg matematičkih pojmova.

Realni brojevi (R)

Definicija: Realni brojevi obuhvaćaju sve racionalne i sve iracionalne brojeve.

$R=Q\cup I$

To znači da je svaki broj koji možemo prikazati na kontinuiranom brojevnom pravcu realan broj. Realni brojevi obuhvaćaju sve prethodno spomenute vrste brojeva i predstavljaju najširi skup brojeva s kojima se najčešće susrećemo u školskom obrazovanju.

Zašto su ovi skupovi važni?

Razumijevanje skupova brojeva ključno je za kasnije teme u matematici, poput rada s jednadžbama, funkcijama i geometrijskim problemima. Jasno poznavanje koji brojevi pripadaju kojem skupu pomaže pri izboru odgovarajućih metoda za rješavanje zadataka te pri komunikaciji matematičkih ideja.

U nadolazećim lekcijama nastavit ćemo širiti i produbljivati razumijevanje ovih pojmova, a istovremeno ćete imati priliku riješiti razne zadatke koji će vam pomoći da primijenite naučeno u praksi.

Responses

Morate biti prijavljeni da biste objavili komentar.

Matematika A razina

O ispitu matematike više razine na maturi